Bereiche der Chemie » Allgemeine Chemie » Atombau » Atommodelle
Elementarteilchen des Atoms Atombau Das Periodensystem
Unterabschnitte

Atommodelle

Planetenmodell von Rutherford

Das Elektron befindet sich wie ein Planet auf einer konstanten Kreisbahn um den Kern. Die elektrische Anziehungskraft (Zentralkraft) muß somit die Zentrifugalkraft genau aufheben (Kräftegleichgewicht). Mit der Zentrifugalkraft wird das Elektron vom Kern weggetrieben:

\begin{displaymath}Zentrifugalkraft=-elektrische\,\,Anziehungskraft\end{displaymath}


\begin{displaymath}F_{Z}=-F_{el}\end{displaymath}

Die elektrostatische Anziehungskraft wird mit Hilfe des Coulombschen Gesetzes beschrieben:

\begin{displaymath}F=f\cdot\frac{Q_{1}\cdot Q_{2}}{r^{2}},\end{displaymath}

Wir setzen ein:
  • Proportionalitätsfaktor f:

    \begin{displaymath}f=\frac{1}{4\pi\cdot\epsilon_{0}}\end{displaymath}

  • $Q_{1},Q_{2}$ die Energie des Protons und des Elektrons, wobei das Elektron negativ ist, das Proton positiv
  • Die elektrische Feldkonstante $\epsilon_{0}$ ist

    \begin{displaymath}\epsilon_{0}=8,854\cdot 10^{-12}A^{2}s^{4}kg^{-1}m^{-3}\end{displaymath}

Somit folgt die Gleichung

\begin{displaymath}F_{el}=\frac{1}{4\pi\epsilon_{0}}\cdot \frac{e\cdot-e}{r^{2}}=\frac{-e^{2}}{4\pi\cdot\epsilon_{0}\cdot r^{2}}\end{displaymath}

Die Zentrifugalkraft ist

\begin{displaymath}F_{Z}=\frac{mv^{2}}{r}\end{displaymath}

Somit folgt:

\begin{displaymath}F_{Z}=-F_{el}\Leftrightarrow \frac{mv^{2}}{r}=-\frac{-e^{2}}{... ...eftrightarrow mv^{2}=\frac{e^{2}}{4\pi\cdot\epsilon_{0}\cdot r}\end{displaymath}

Schalenmodell von Bohr

Verschiedene Versuche ließen sich nicht mit dem von Rutherford entwickelten Atommodell erklären. Zum Beispiel sind die Spektren von Wasserstoffatomen und von anderen Atomen nicht erklärbar. Weiterhin war auch dieses Atommodell nur im Einklang zur klassischen Mechanik, aber im Wiederspruch zur klassischen Elektrodynamik, da das Elektron laufend Energie verlieren müßte und in den Kern spriralförmig stürzen müßte, was es aber nicht tut.
Niels Bohr postulierte, daß sich das Elektron nur auf bestimmten Bahnen im Atom bewegen kann. Er postulierte, daß auf diesen Bahnen das Elektron keine Energie verliert. Diese Bahnen sind solche bei denen die Energie des Elektrons ein ganzzahliges Vielfaches des Bahndrehimpluses ist:

\begin{displaymath}mvr=n\cdot\frac{h}{2\pi},\end{displaymath}

wobei $n$ ganzzahlig und positiv ist3. $h$ ist das planksche Wirkumsquantum. Es ist ein fester Wert und beträgt:

\begin{displaymath}h=6,626\cdot10^{-34}kg\,m^{3}s^{-1}\end{displaymath}

Nun formt man diese Gleichung nach $v$ um und erhält:

\begin{displaymath}v=\frac{nh}{2\pi mr}\end{displaymath}

Setzt man nun diese Gleichung in die Balance-Gleichung zwischen Zentrifugalkraft und elektrischer Anziehungskraft ein und löst nach $r$ auf, so erhält man den Bohrschen Atomradius und kann berechnen auf welchen Bahnen sich die Elektronen um den Kern nach dem Modell bewegen müssen:

\begin{displaymath}r=\frac{h^{2}\epsilon_{0}}{\pi me^{2}}\cdot n^{2}=n^{2}\cdot 0,53\cdot10^{-10}m\end{displaymath}

Erklärung des Spektrums der Wasserstoffatome mit der Bohrschen Theorie

Mit Hilfe des Schalenmodells gelingt es uns, die Wellenspektren des Wasserstoffatoms zu erklären. Hierfür berechnen wir zunächst die Engerie eines Elektrons. Diese setzt sich zusammen aus potenzieller Energie und kinetischer Energie

\begin{displaymath}E=E_{kin}+E_{pot}\end{displaymath}

Die kinetische Engerie ist die Energie, die durch die Bewegung des Elektrons zustandekommt

\begin{displaymath}E_{kin}=\frac{mv^{2}}{2}\end{displaymath}

Die potenzielle Energie ist die Energie, die durch die elektrische Anziehung zustandekommt

\begin{displaymath}E_{pot}=\int_{\infty}^{r}\frac{e^{2}}{4\pi\epsilon_{0}r^{2}}=-\frac{e^{2}}{4\pi\epsilon_{0}r}\end{displaymath}

Man erhält

\begin{displaymath}E=E_{kin}+E_{pot}=\frac{mv^{2}}{2}-\frac{e^{2}}{4\pi\epsilon_... ...rac{e^{2}}{4\pi\epsilon_{0}r}=-\frac{e^{2}}{8\pi\epsilon_{0}r}.\end{displaymath}



Wir setzen $r=\frac{h^{2}\epsilon_{0}}{\pi me^{2}}\cdot n^{2}$ für den Bohrschen Radius in die Gleichung ein und erhalten

\begin{displaymath}E=-\frac{e^{2}}{8\pi\epsilon_{0}\cdot\frac{h^{2}\epsilon_{0}}... ...{2}}=-\frac{me^{4}}{8\epsilon_{0}^{2}h^{2}}\cdot\frac{1}{n^{2}}\end{displaymath}

für die möglichen Energiewerte des Elektrons.

Regt man Wasserstoffatome an, so strahlen sie Licht aus. Dieses Licht hat jedoch nicht das gesamte Spektrum, sondern es besteht aus Spektrallinien: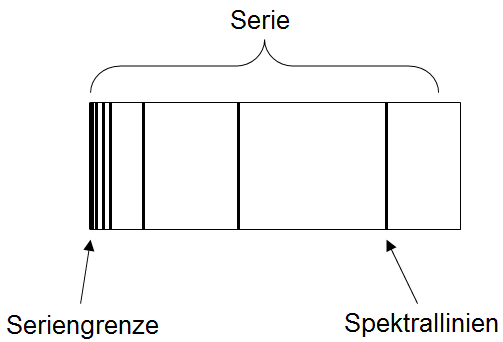
Spektrallinien
In diesem Schaubild wird die Energie nach links hin immer höher. Dies schlägt sich in einer kürzeren Wellenlänge aus. Nach rechts hin wird die Energie immer geringer, die Wellen werden länger.

Es gibt verschiedene Serien: Die Balmerserie im sichtbaren Bereich, die Lyman-Serie im ultravioletten Bereich, sowie die Paschen und Bracket Serien im infraroten Bereich: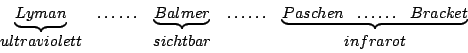

Lyman im ultravioletten Bereich, Balmer im sichtbaren, Paschen und Bracket im infraroten Bereich

Schon früh hatte Rydberg die Beziehung

\begin{displaymath}\frac{1}{\lambda}=R_{\infty}\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)\end{displaymath}

aufgestellt, wobei $R_{\infty}$ die Rydbergkonstante $R_{\infty}=109678cm^{-1}$ und $\lambda$ die Wellenlänge des Lichtes ist.
Die Rydbergkonstante läßt sich nun nicht nur wie von Rydberg experimentell bestimmen, sondern sie läßt sich berechnen:

\begin{displaymath}E=E_{2}-E_{1}=\left(-\frac{me^{4}}{8\epsilon_{0}^{2}h^{2}}\cd... ...silon_{0}^{2}h^{2}}\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right)\end{displaymath}

Durch Einsetzen der Planckschen Gleichung

\begin{displaymath}E=hc\cdot\frac{1}{\lambda}\end{displaymath}

für $E$ erhält man für $m>n$

\begin{displaymath}hc\cdot\frac{1}{\lambda}=\frac{me^{4}}{8\epsilon_{0}^{2}h^{2}... ...lon_{0}^{2}h^{3}c}\left(\frac{1}{n^{2}}-\frac{1}{m^{2}}\right).\end{displaymath}

Mit Hilfe der Bohrschen Theorie ist es uns gelungen eine Erklärung für die Spektren der Wasserstoffatome zu finden. Die Elektronen der Wasserstoffatome können nur in ganz bestimmten Energiezuständen sich befinden. Wechseln sie von einem höheren Energiezustand zu einem niederen Energiezustand, so tun sie dies sprunghaft und strahlen dabei einen Lichtquanten mit einer bestimmten Wellenlänge ab, welche man dann im Spektrum sehen kann.

Wellenmechanisches Atommodell

Mit dem Bohrschen Atommodell waren zwar einfache Wasserstoffatome erklärbar geworden, aber Atome mit mehr Elektronen waren nicht erklärbar. Broglie, Heisenberg, Schrödinger u.a. schufen deshalb ein leistungsfähigeres Atommodell: Das Wellenmechanische Atommodell.
Heisenberg stellte die Unbestimmtheitsbeziehung

\begin{displaymath}\Delta q\cdot\Delta(m\cdot v)\geq \frac{h}{4\pi}\end{displaymath}

auf, die sagt, daß es unmöglich ist, Ort und Drehimpuls des Elektrons gleichzeitig zu bestimmen. Es ist in dem modernen Atommodell hinfort unmöglich genau zu sagen, wo sich ein Elektron befindet. Das Elektron umkreist nicht mehr in vorher genau festgelegten Bahnen den Atomkern, sondern es ist in einem (kleinen) Bereich der Elektronenhülle mit einer bestimmten Wahrscheinlichkeit anzutreffen. Die Aufenthaltswahrscheinlichkeit eines Elektrons in der Kugel vom Radius $r$ ist beispielsweise

\begin{displaymath}\int^{r}_{r=0}\Psi^{2}4\pi r^{2}dr.\end{displaymath}

Hierbei sinkt die Wahrscheinlichkeit des Antreffens mit der Entfernung vom Kern laufend ab, wird aber nicht $0$. Somit ist ein Atom auch ein nie endendes Gebilde. Man kann aber trotzdem Grenzen zeichnen, indem man die einen Atomkern umgebende Elektronenwolke nur bis zu einer bestimmten Wahrscheinlichkeit zeichnet.

Zusätzlich zu der Unbestimmtheitsbeziehung kommt noch der Wellencharakter des Elektrons. Ein Elektron kann eine Welle oder ein Teilchen sein, je nachdem aus welcher Sichtweise man es betrachtet. Das Elektron legt sich als eine dreidimenional stehende Welle um den Atomkern. Hierbei können nur solche Wellen ,,stehen'', welche sich nicht selbst zerstören, d.h. wenn die Welle um den Atomkern einmal ,,rum'' ist, dann muß sie die selben Schwingungen haben, wie das andere Ende der Welle, um sich am Anfang der Welle nicht auszugleichen. Zwischen Wellenlänge und Impuls eines Teilchens besteht die Beziehung (de Broglie-Beziehung)

\begin{displaymath}\lambda=\frac{h}{mv}.\end{displaymath}

Ein ganzes Vielfaches der Wellenlänge muß exakt die Kreisbahn ergeben:

\begin{displaymath}n\lambda=2\pi r\end{displaymath}

Setzt man die erste Formel in die letzte ein, so erhält man wieder die von Bohr willkürlich postulierte Quantelung des Drehimpulses:

\begin{displaymath}n\cdot\frac{h}{mv}=2\pi r\Leftrightarrow n\cdot\frac{h}{2\pi}=mvr\end{displaymath}

Die vier Quantenzahlen

Schrödinger stellt die berühmte Wellengleichung auf, welche die dreidimensionalen Wellen eines Atoms berechnen kann. Bei dem lösen dieser Schrödingergleichung ergeben sich vier Quantenzahlen:

Quantenzahl Werte Beschreibung
Hauptquantenzahl $(n)$ $1\ldots\infty$ Bestimmt die größe der Orbitale. Ist gleichzusetzen mit der Energie des Elektrons $E_{n}=-\frac{me^{4}}{8\epsilon_{0}^{2}h^{2}}\frac{1}{n^{2}}$
Nebenquantenzahl $(l)$ $0\ldots n-1$ Bestimmt die Geometrie der Orbitale.
  • 0=s (Kugel)
  • 1=p (Hantel)
  • 2=d (zwei Hanteln nahezu senkrecht - bei den meisten Orbitalen dieser Art)
  • 3=f (noch eine dritte dazu)
Magnetquantenzahl $(m_{l})$ $-l\ldots+l$ Gibt an wieviele Oribitale von dem durch die Nebenquantenzahl bestimmten Typ vorhanden sind.
  • s: 1
  • p: 3
  • d: 5
  • f: 7
Spinquantenzahl $(m_{s})$ $-\frac{1}{2},+\frac{1}{2}$ Gibt den Eigendreh-Spin des Elektrons an. Jedes Elektron kann entweder ,,linksherum'' oder ,,rechtsherum'' sich drehen.

Schrödingergleichung

Die Schrödingergleichung sieht folgendermaßen aus: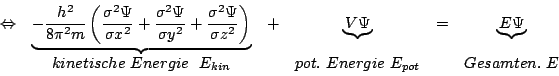

\begin{displaymath}\frac{\sigma^{2}\Psi}{\sigma x^{2}}+\frac{\sigma^{2}\Psi}{\si... ...sigma^{2}\Psi}{\sigma z^{2}}+\frac{8\pi^{2}m}{h^{2}}(E-V)\Psi=0\end{displaymath}


\begin{displaymath}\Leftrightarrow\frac{\sigma^{2}\Psi}{\sigma x^{2}}+\frac{\sig... ...\sigma^{2}\Psi}{\sigma z^{2}}=-\frac{8\pi^{2}m}{h^{2}}(E-V)\Psi\end{displaymath}


\begin{displaymath}\Leftrightarrow-\frac{h^{2}}{8\pi^{2}m}\left(\frac{\sigma^{2}... ...gma y^{2}}+\frac{\sigma^{2}\Psi}{\sigma z^{2}}\right)=(E-V)\Psi\end{displaymath}


\begin{displaymath}\begin {array}{cccccc} \Leftrightarrow&\underbrace{-\frac{h^... ...n}&&pot.\,\, Energie\,\,E_{pot}&&Gesamten.\,\,E\\ \end{array}\end{displaymath}

wobei
$V$: potenzielle Energie des Elektrons
$m$: Masse des Elektrons
$h$: Plankkonstante
$E$: Elektronenergie
und $\Psi$: die Wellenfunktion.

Einfacher schreibt man

\begin{displaymath}H\Psi=E\Psi\end{displaymath}

wobei
$H$: der Hamiltonoperator
$E$: Elektronenergie
und $\Psi$: die Wellenfunktion.

Die durch die Lösung der Schrödingergleichung entstehenden Wellenfunktionen 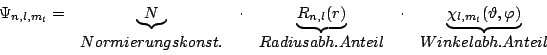$\Psi$ werden Eigenfunktionen genannt. Um diese Wellenfunktion besser anschaulich zu machen, wird sie in Kugelkoordinaten4 dargestellt und besteht anschließend aus einer Radialfunktion und einer Winkelfunktion, welche mit eier Normierungskonstante normiert werden.

\begin{displaymath} \begin {array}{cccccc} \Psi_{n,l,m_{l}}=&\underbrace{N}&\c... ...ngskonst.&&Radiusabh. Anteil&&Winkelabh. Anteil\\ \end{array}\end{displaymath}

Ein Beispiel für eine solche Funktion ist die Winkelfunktion für das $2s$-Orbital. Hier ist der normierte Radialanteil5

\begin{displaymath}\frac{1}{2\sqrt{2a_{0}^{3}}}\left(2-\frac{r}{a_{0}}\right) e^{- \frac{r}{2a_{0}}} \end{displaymath}

und der normierte Winkelanteil

\begin{displaymath}\frac {1}{2\sqrt{\pi}}.\end{displaymath}

Der radiale Anteil zusammen mit der Dichte6 gezeichnet. Die Nullpunkte sind die Knotenflächen des Oribtals7: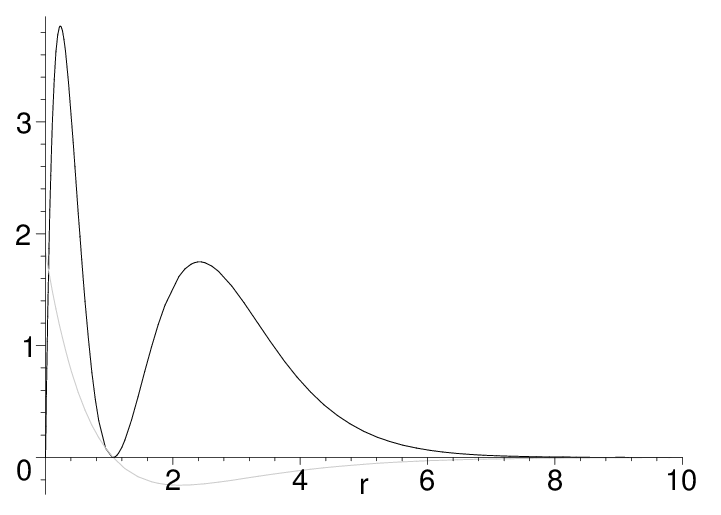



Aus den unterschiedlichen Eigenfunktionen ergeben sich die Atomorbitale. Einige Atomorbitale sind unten in der Grafik aufgezeichnet.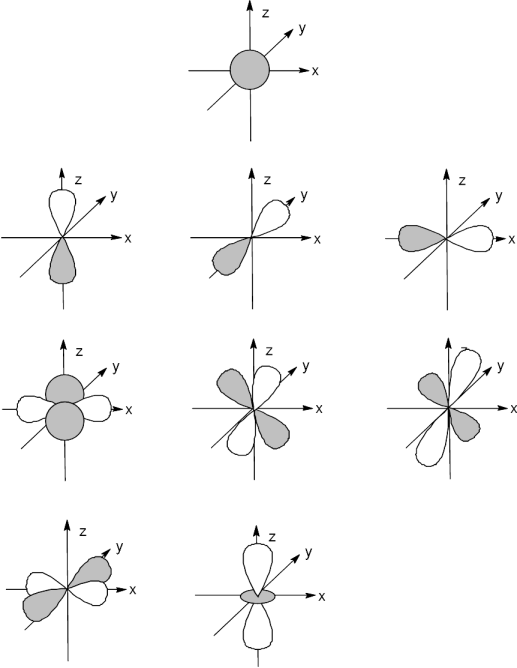

Atomorbitale Übersicht
Von links nach rechts, von oben nach unten:
$s$-Orbital,
$p_{z}$-Orbital, $p_{y}$-Orbital, $p_{x}$-Orbital,
$d_{xy}$-Orbital, $d_{xz}$-Orbital, $d_{yz}$-Orbital, $d_{x^{2}-y^{2}}$-Orbital, $d_{z^{2}}$-Orbital.


Zur Ergänzung und weiterer Verdeutlichung eine weitere Darstellung: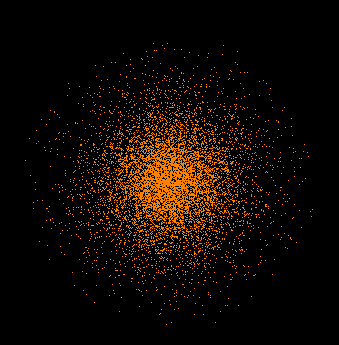

Punktwolke des 1s-Orbitals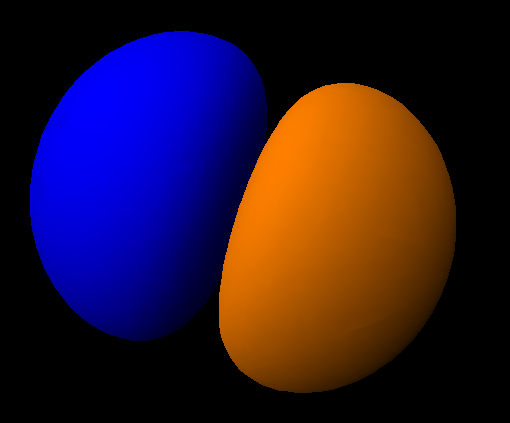
Punktwolke des 1s-Orbitals


Eines der drei 2p-Orbitale
Darstellung eines der drei 2p-Orbitale. Diesmal nicht mehr als Punktwolke,
sondern bei einer bestimmten Wahrscheinlichkeit abgeschlossen.




Das $d_{z^{2}}$-Orbital in einem kurzen Video.
Ganz besonders deutlich wird der Leerraum im Zentrum.
Hier herunterladen
Spielbar mit dem Quicktime-Player.


Elementarteilchen des Atoms Atombau Das Periodensystem