Bereiche der Chemie » Anorganische Chemie » Elektrolyse/Galvanisches Element » Galvanisches Element
Elektrolyse Elektrolyse/Galvanisches Element
Unterabschnitte

Galvanisches Element

Schaubild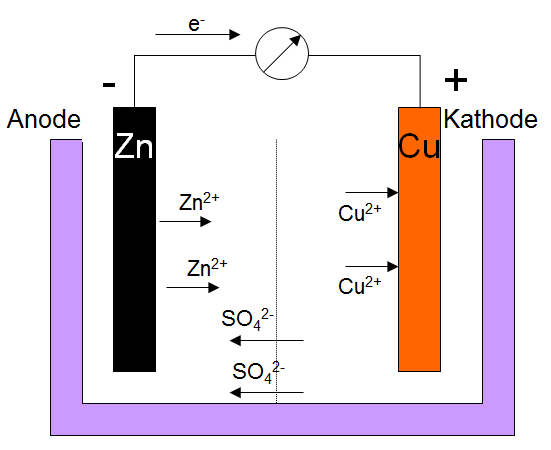

Batterie/Akkumulator

Eine Batterie ist ein galvanisches Element. Im Handel sind viele verschiedene Batterien. Eine Batterie kann jedoch nicht wieder geladen werden, während in einem Akkumulator auch eine Elektrolyse zum wiederbeladen desselben stattfinden kann. Somit kann man das System Galvanisches Element/Elektrolyseelement als Stromspeicher verwenden.

Normalwasserstoffhalbzelle

Die Normalwasserstoffhalbzelle besteht aus einer platinierten Platinelektrode über die in Wasser Wasserstoff mit einem Druck von $1013hPa$ geblasen wird. Die Zelle wird mit einer Salzbrücke, daß ist ein Glasrohr mit einer Salzlösung gefüllt und an beiden Enden mit einem Diaphragma verschlossen, mit einer anderen Halbzelle verbunden.
Nun kann der Strom fließen und zwar fließt er entweder von der Normalwasserstoffhalbzelle in die andere Zelle, dann ist die Normalwasserstoffhalbzelle die Anode und das Redoxpotential der anderen Zelle ist positiv oder der Strom fließt von der anderen Zelle in die Normalwasserstoffhalbzelle. Hierbei ist die Normalwasserstoffhalbzelle die Kathode und das Redoxpotential der anderen Zelle ist negativ.

Spannungsreihe

In der Spannungsreihe sind die Standardpotentiale der Normalwasserstoffhalbzelle gegenüber anderen Halbzellen aufgetragen. Aus dieser Gleichung kann man ablesen, wie die einzelnen Zellen unter Normalbedingungen miteinander reagieren. Die Spannung zwischen den einzelnen Zellen wird die Differenz der Standardpotentiale unter Normalbedingungen sein. Hier ein Ausschnitt aus der Tabelle:

Reduzierte Form Oxidierte Form Standardpotential $E^{0}$ in $V$
$Na$ $Na^{+}$ $-2,71$
$Zn$ $Zn^{2+}$ $-0,76$
$Cd$ $Cd^{2+}$ $-0,40$
$H_{2}+2H_{2}O$ $2H_{3}O^{+}$ $0$
$Cu$ $Cu^{2+}$ $+0,34$
$2Cl^{-}$ $Cl_{2}$ $+1,36$
$2F^{-}$ $F_{2}$ $+2,87$

Berechnung von Redoxpotentialen mit Hilfe der Nernstschen Gleichung

Die Nernstsche Gleichung lautet

\begin{displaymath}E=E_{0}+\frac{RT}{zF}lg\frac{c_{Ox}}{c_{Red}}\end{displaymath}

$R$ ist dabei die Gaskonstante, $T$ die Temperatur und $F$ die Faradaykonstante. $z$ ist die Anzahl der Elektronen, die bei der Redoxgleichung mitspielen:

\begin{displaymath}Red\rightleftharpoons Ox+ze^{-}\end{displaymath}

Nachdem man die Konstanten zusammenfaßt und auch die Temperatur auf die Normaltemperatur von $25^{\circ}C$ setzt erhält man

\begin{displaymath}E=E_{0}+\frac{0,059(V)}{z}lg\frac{c_{Ox}}{c_{Red}}\end{displaymath}

Beim Einsetzen in die Nernstsche Gleichung muß man darauf achten, daß die Konzentrationen fester Reaktionspartner immer gleich 1 sind. Dies sind die Elektronen.
Beispiel:
Eine Kupferhalbzelle hat eine Konzentration von Kupfersulfit $CuSO{3}$ von $2\frac{mol}{l}$ und die Redoxgleichung ist wie folgt:

\begin{displaymath}Cu\rightleftharpoons Cu^{2+}+2e^{-}\end{displaymath}

Somit ist das Potential dieser Halbzelle

\begin{displaymath}E=E_{0}+\frac{0,059V}{2}lg\frac{2 mol/l}{1 mol /l}=0,34V+0,0295V \cdot 0,30=0,3488 V\end{displaymath}

Elektrolyse Elektrolyse/Galvanisches Element